21 января 2021 года
Группа 108
Предмет :"Математика"
Тема урока :"Пирамида, ее осно
Пирамида - (от греч. pyramis, род. п. pyramidos), многогранник,
основание которого многоугольник, а остальные грани треугольники, имеющие
общую вершину. По числу углов основания различают пирамиды треугольные,
четырехугольные и т. д.
Общая вершина боковых граней называется вершиной пирамиды. Высотой
пирамиды называется перпендикуляр, опущенный из вершины пирамиды на
плоскость основания. - Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса.
Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основани
Элементы пирамиды- апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины[3];
- боковые грани — треугольники, сходящиеся в вершине пирамиды;
- боковые ребра — общие стороны боковых граней;
- вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;
- высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра);
- диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;
- основание — многоугольник, которому не принадлежит вершина пирамиды
- Свойства пирамиды
Если все боковые ребра равны, то: - около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр;
- боковые ребра образуют с плоскостью основания равные углы.
- также верно и обратное, то есть если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
Если боковые грани наклонены к плоскости основания под одним углом, то:
- в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр;
- высоты боковых граней равны;
- площадь боковой поверхности равна половине произведения периметра
- Объём пирамиды может быть вычислен по формуле:
 - где
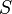 — площадь основания и — площадь основания и 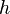 — высота; — высота;
- Боковая поверхность — это сумма площадей боковых граней:

- Полная поверхность — это сумма площади боковой поверхности и площади основания:

- Для нахождения боковой поверхности в правильной пирамиде можно использовать формулы:
 - где
 — апофема , — апофема ,  — периметр основания, — периметр основания,  — число сторон основания, — число сторон основания,  — боковое ребро, — боковое ребро,  — плоский угол при вершине пирамиды. — плоский угол при вершине пирамиды.
Особые случаи пирамидыПравильная пирамидаПирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами: - боковые ребра правильной пирамиды равны;
- в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
- в любую правильную пирамиду можно как вписать, так и описать около неё сферу;
- если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна
 , а каждый из них соответственно , а каждый из них соответственно  , где n — количество сторон многоугольника основания[6]; , где n — количество сторон многоугольника основания[6];
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Прямоугольная пирамидаПирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды. Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию. основания на высоту боковой грани.
|
вание, высота, боковая поверхность"
Комментариев нет:
Отправить комментарий