19 января 2021 года

Группа 108

Предмет :"Мамематика"

Тема занятия :"Теорема Эйлера. Прямая и н

Основные определения и свойства призм. Теорема Эйлера

      Определение 1. Рассмотрим две паралллельные плоскости   α   и   β ,   прямую   p ,   пересекающую эти плоскости, и произвольный выпуклый n – угольник   A₁A₂ ... A_n ,   лежащий в плоскости   α   (рис. 1).

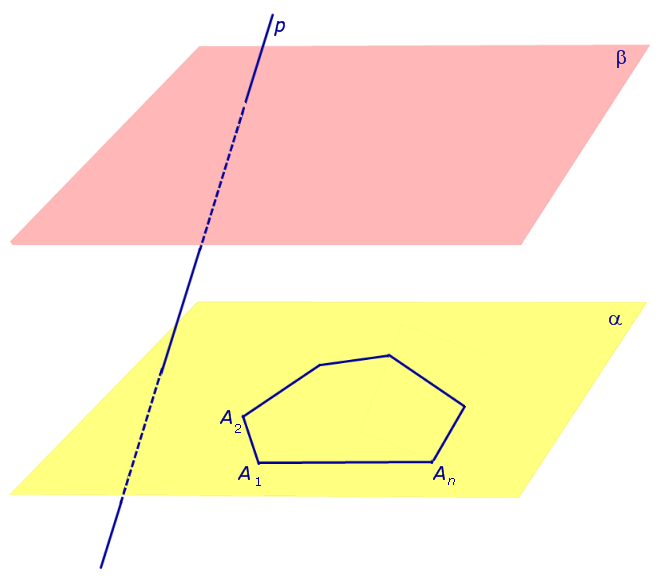
Рис.1

      Если через каждую точку многоугольника   A₁A₂ ... A_n   провести прямую, параллельную прямой   p ,   и обозначить символами   A'₁, A'₂, ... , A'_n   точки пересечения с плоскостью   β   прямых, параллельных прямой   p   и проходящих через точки   A₁, A₂, ... , A_n,   то полученную фигуру   A₁A₂ ... A_n A'₁A'₂ ... A'_n   называют n – угольной призмой (рис.2).

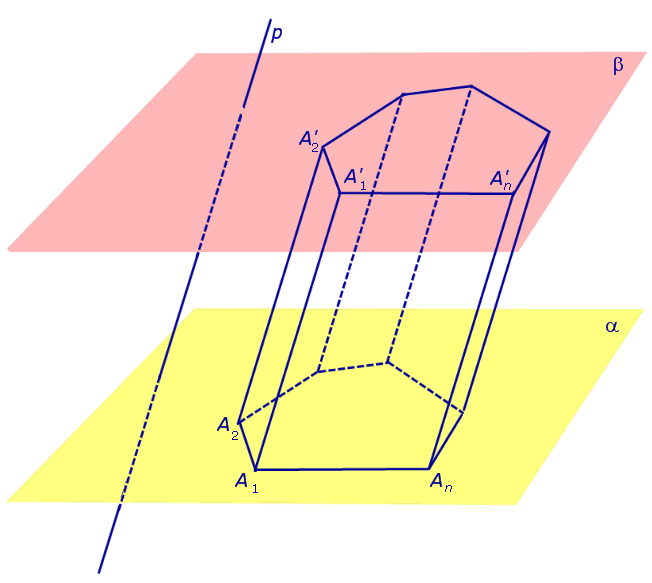
Рис.2

      Утверждение 1. Каждый из   n   четырехугольников

A₁A₂A'₂A'₁,   A₂A₃A'₃A'₂,   ... ,   A_nA₁A'₁A'_n

является параллелограммом.

      Доказательство. Докажем сначала, что параллелограммом является, например, четырехугольник   A₁A₂A'₂A'₁.   Для этого заметим, что стороны   A₁A'₁   и   A₂A'₂   параллельны по построению. Заметим также,что прямая   A₁A₂   параллельна плоскости   β ,   так как лежит в плоскости α ,   которая параллельна плоскости   β .   Прямая A'₁A'₂   является линией пересечения плоскости   A₁A₂A'₂A'₁   с плоскостью   β .   Из признака параллельности прямой и плоскости следует, что прямая   A'₁A'₂   параллельна прямой   A₁A₂ .   Таким образом, у четырехугольника   A₁A₂A'₂A'₁   противоположные стороны попарно параллельны, то есть   A₁A₂A'₂A'₁   – параллелограмм.

     Для остальных четырехугольников доказательство проводится аналогично.

      Определение 2. Параллелограммы

A₁A₂A'₂A'₁,   A₂A₃A'₃A'₂,   ... ,   A_nA₁A'₁A'_n

называют боковыми гранями призмы. Совокупность всех боковых граней призмы составляет боковую поверхность призмы.

     Определение 3. Многоугольники   A₁A₂ ... A_n   и   A'₁A'₂ ... A'_n   называют основаниями призмы.

     Определение 4. Точки   A₁, A₂, ... , A_n , A'₁, A'₂, ... , A'_n   (вершины многоугольников   A₁A₂ ... A_n   и   A'₁A'₂ ... A'_n )   называют вершинами призмы.

     Определение 5. Отрезки   A₁A'₁ , A₂A'₂ , ... , A_nA'_n   называют боковыми ребрами призмы.

      Утверждение 2 . Все боковые ребра призмы равны.

      Это утверждение непосредственно вытекает из утверждения 1.

      Определение 6. Отрезки   A₁A₂ , A₂A₃ , ... , A_nA₁ , ... , A'₁A'₂ , A'₂A'₃ , ... , A'_nA'₁   (стороны многоугольников   A₁A₂ ... A_n   и   A'₁A'₂ ... A'_n )   называют ребрами оснований призмы.

      Замечание 1. В случае, когда не требуется делать специальных уточнений,

	боковые ребра и ребра оснований называют ребрами призмы,
	боковые грани и основания призмы называют гранями призмы
	совокупность всех граней призмы (всех боковых граней и оснований) называют полной поверхностью призмы,
	n – угольные призмы называют призмами.

      Теорема Эйлера . Для любой призмы справедливо равенство:

число вершин

+

число граней

–

число ребер

=

2

      Доказательство. Заметим, что у n – угольной призмы   2n   вершин,   n   боковых граней,   2   основания,   2n   ребер основания и   n   боковых ребер. Следовательно, у n – угольной призмы   (n + 2)   грани и   3n   ребер.

      Поскольку

2n + (n + 2) – 3n = 2

то теорема Эйлера доказана.

      Определение 7. Расстояние между плоскостями, на которых лежат основания призмы, называют высотой призмы.

      Замечание 2. С различными формулами для вычисления объема призмы и площадей боковой и полной поверхности призмы можно ознакомиться в разделе «Формулы для объема, площади боковой поверхности и площади полной поверхности призмы».

     Замечание 3. С определением сечения призмы и способами построения сечений призмы ожно ознакомиться в разделе «Сечения призмы. Перпендикулярные сечения призмы».

Виды призм. Прямые и наклонные призмы. Правильные призмы

      Существует следующая классификация призм.

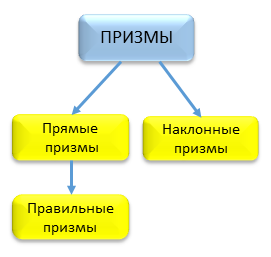
Рис.3

      Определение 8. Прямой призмой называют призму, боковые ребра которой перпендикулярны к плоскостям оснований. Призмы, боковые ребра которых не перпендикулярны к плоскостям оснований, называют наклонными призмами.

      Замечание 4. Все боковые грани прямой призмы являются прямоугольниками. Высота прямой призмы равна длине бокового ребра.

      Определение 9. Правильной призмой называют прямую призму, основаниями которой служат правильные многоугольники.

      Определение 10. Диагональю призмы называют отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Примеры призм. Треугольные призмы. Четырехугольные призмы.
Параллелепипеды

Призма	Рисунок	Свойства
Наклонная треугольная призма		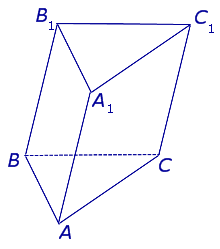Боковые ребра   AA1, BB1, CC1 не перпендикулярны плоскостям  ABС   и   A1B1C1. ABС – произвольный треугольник.
Прямая треугольная призма		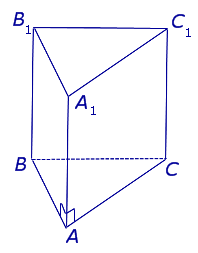Боковые ребра   AA1, BB1, CC1   перпендикулярны плоскостям  ABС   и   A1B1C1. ABС – произвольный треугольник. Боковые грани прямой треугольной призмы – прямоугольники. Высота прямой треугольной призмы равна длине бокового ребра.
Правильная треугольная призма		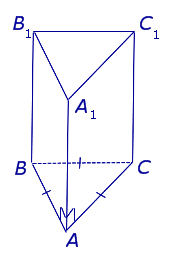Боковые ребра   AA1, BB1, CC1   перпендикулярны плоскостям  ABС   и   A1B1C1. ABС   – равносторонний треугольник. Боковые грани правильной треугольной призмы – прямоугольники. Высота правильной треугольной призмы равна длине бокового ребра.
Наклонная четырехугольная призма		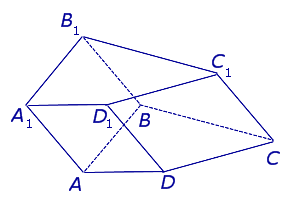Боковые ребра   AA1, BB1, CC1, DD1 не перпендикулярны плоскостям   ABСD   и   A1B1C1D1. ABСD – произвольный четырехугольник.
Прямая четырехугольная призма		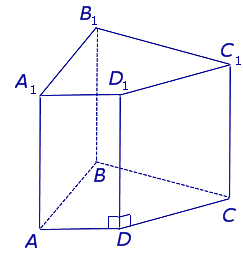Боковые ребра   AA1, BB1, CC1, DD1   перпендикулярны плоскостям   ABСD   и   A1B1C1D1. ABСD – произвольный четырехугольник. Боковые грани прямой четырехугольной призмы – прямоугольники. Высота прямой четырехугольной призмы равна длине бокового ребра.
Правильная четырехугольная призма		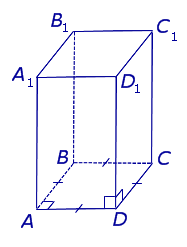Боковые ребра   AA1, BB1, CC1, DD1   перпендикулярны плоскостям   ABСD   и  A1B1C1D1. ABСD – квадрат. Боковые грани правильной четырехугольной призмы – прямоугольники. Высота правильной четырехугольной призмы равна длине бокового ребра.
Параллелепипед		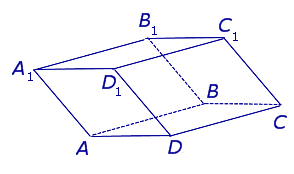Наклонная четырехугольная призма, все грани которой паралллелограммы. Противоположные грани параллелепипеда равны.
Прямой параллелепипед		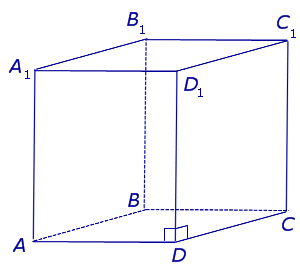Прямая четырехугольная призма, основания  ABСD   и   A1B1C1D1 которой – параллелограммы. Высота прямого параллелепипеда равна длине бокового ребра.
Прямоугольный параллелепипед		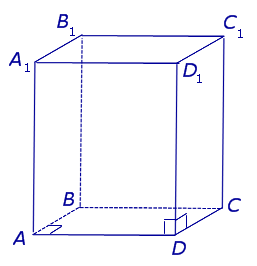Прямая четырехугольная призма, основания   ABСD   и   A1B1C1D1   которой – прямоугольники. Все грани прямоугольного параллелепипеда являются прямоугольниками.
Правильный параллелепипед		Синоним термина «правильная четырехугольная призма» Основания  ABСD   и   A1B1C1D1   – равные квадраты, боковые грани – равные прямоугольники. Высота правильного параллелепипеда равна длине бокового ребра.
Куб		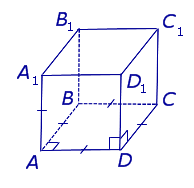Правильный параллелепипед, у которого все грани равные квадраты. У куба все ребра равны и попарно перпендикулярны. Высота куба равна длине ребра.

аклонная призма"