09 декабря 2020

Группа 108

Предмет :" Математика"

Тема урока:"Использование

Тема 4.3. Использование свойств и графиков функций при решении уравнений и неравенств.

Графическое решение уравнений с одной переменной.

На практике довольно часто оказывается, что решение уравнения  сопряжено с громоздкими выкладками. В таких случаях прибегают к тому или иному методу приближенного решения уравнения. Мы рассмотрим графический метод, который, хотя и не обеспечивает хорошей точности, но является одним из наиболее простых. Он заключается в следующем: строят график функции  и находят абсциссы точек пересечения графика с осью  . Так, для решения уравнения  достаточно построить график функции  и найти абсциссы точек пересечения этого графика с осыо  .

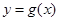Однако во многих случаях указанный выше метод графического решения уравнения не очень удобен. Так, для нахождения корней уравнения  потребовалось бы построить график функции  , а это достаточно трудная задача. В подобных случаях уравнение  преобразуют к виду  , затем строят графики функций  и  (если, разумеется, это проще, чем построение графика функции  ) и находят абсциссы точек пересечения построенных графиков.

Так, для решения уравнения  можно преобразовать уравнение к виду  , затем построить графики функций  и  и найти абсциссы точек пересечения этих графиков.

Ясно, что уравнение  может быть преобразовано к виду  разными способами. Например, уравнение  можно преобразовать в одно из следующих уравнений:  ,  ,  .

В первом случае надо строить графики функций  и  , во втором  и  , в третьем  и  .

Пример 1. Решить графически уравнение  .

Заданное уравнение целесообразно переписать в виде  . Теперь решение уравнения может быть сведено к нахождению абсцисс точек пересечения графиков функций  и  . На рис. 1 в одной системе координат построены графики функций  и  . Определяем абсциссы точек А и В пересечения этих графиков  ;  . Таким образом, заданное

уравнение имеет два корня: -1; 2.

Пример 2. Решить графически уравнение  .

Построим в одной системе координат графики функций  и  (рис. 2). Они пересекаются в точке А, абсцисса которой приближенно равна 1,3. Значит, заданное уравнение имеет единственное решение  .

Метод интервалов.

Множество решений уравнений и неравенств с двумя переменными и их систем.

Графическое решение систем уравнений

Решить графически систему уравнений - это значит найти координаты общих точек графиков уравнений, построенных в одной системе координат.

Графическое решение системы неравенств

Решить графически систему неравенств – это значит найти область решений, координаты которой будут удовлетворять всем неравенствам системы.

Примеры выполнения заданий. свойств и графиков функции для решения уравнений и неравенств"