03 декабря 2020
Группа 108
Предмет :"Математика"
Тема урока :"Решение тригонометрически
Примеры решения простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами называются неравенства вида
,
,
,
,
где – один из знаков
,
.
Вы должны прежде, конечно, хорошо ориентироваться в тригонометрическом круге и уметь решать простейшие тригонометрические уравнения (часть I, часть II).
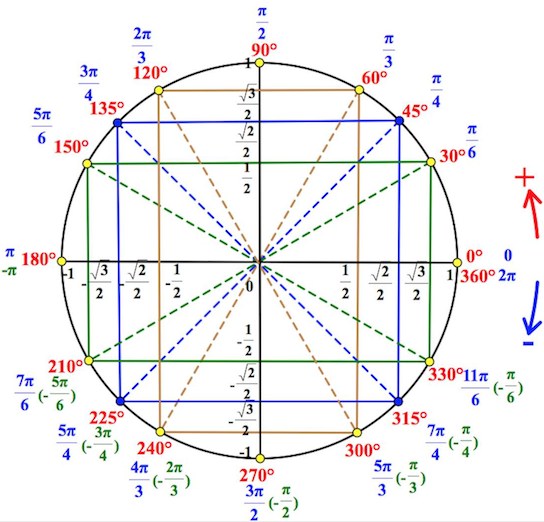
Кстати, умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.
Сначала мы рассмотрим простейшие тригонометрические неравенства с синусом и косинусом. Во второй части статьи – с тангенсом, котангенсом.
Пример 1.
Решить неравенство:
Решение:
Отмечаем на оси косинусов
Все значения , меньшие
– левее точки
на оси косинусов.
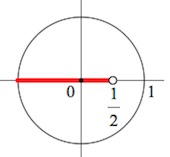
Отмечаем все точки (дугу, точнее – серию дуг) тригонометрического круга, косинус которых будет меньше
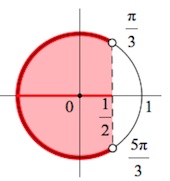
Полученную дугу мы проходим против часовой стрелки (!), то есть от точки до
.
Обратите внимание, многие, назвав первую точку вместо второй точки
указывают точку
, что неверно!
Становится видно, что неравенству удовлетворяют следующие значения
Следите за тем, чтобы «правая/вторая точка» была бы больше «левой/первой».
Не забываем «накидывать» счетчик
Вот так выглядит графическое решение неравенства не на тригонометрическом круге, а в прямоугольной системе координат:

Пример 2.
Решить неравенство:
Решение:
Отмечаем на оси косинусов
Все значения , большие или равные
– правее точки
, включая саму точку.
Тогда выделенные красной дугой аргументы отвечают тому условию, что
.
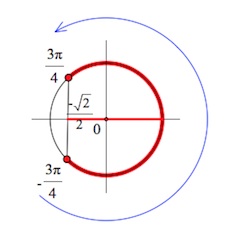
Пример 3.
Решить неравенство:
Решение:
Отмечаем на оси синусов
Все значения , большие или равные
– выше точки
, включая саму точку.
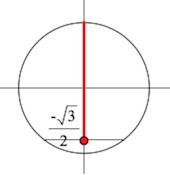
«Транслируем» выделенные точки на тригонометрический круг:
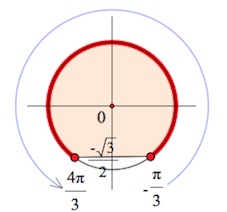
Пример 4.
Решить неравенство:
Решение:
Кратко:
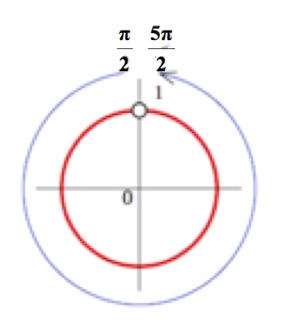
или все , кроме
Пример 5.
Решить неравенство:
Решение:
Неравенство равносильно уравнению
, так как область значений функции
–
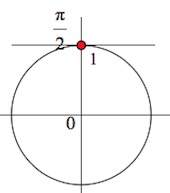
Пример 6.
Решить неравенство:
Решение:
Действия – аналогичны применяемым в примерах выше. Но дело мы имеем не с табличным значением синуса.
Здесь, конечно, нужно знать определение арксинуса.
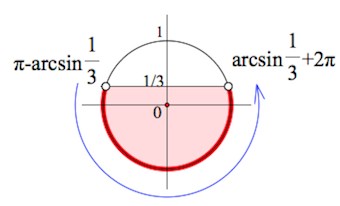
Если не очень понятно, загляните сюда –>+ показать
Тренируемся в решении простейших тригонометрических неравенств
Имейте ввиду, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. Например, в задании 2 ответ можно было записать и так:
1. Решить неравенство:
Ответ: + показать
2. Решить неравенство:
Ответ: + показать
3. Решить неравенство:
Ответ: + показать
4. Решить неравенство:
Ответ: + показать
5. Решить неравенство:
Ответ: + показать
Часть 2
Если у вас есть вопросы, – пожалуйста, – спрашивайте!

х неравенств"
Комментариев нет:
Отправить комментарий