09.11.2020
Группа 108
Предмет:"Математика"
Тема:"Тригонометрические уравнения и приемы и Решение уравнений разложением на множители
sin 4x = 3 cos 2x
Для решения уравнения воспользуемся формулой синуса двойного угла sin 2![]() = 2 sin
= 2 sin![]() cos
cos![]()
2 sin 2x cos 2x – 3 cos 2x = 0,
cos 2x (2 sin 2x – 3) = 0. Произведение этих множителей равно нулю, если хотя бы один из множителей будет равен нулю.
2x =![]() +
+ ![]() к, к
к, к ![]() Z или sin 2x = 1,5 – нет решений, т.к | sin
Z или sin 2x = 1,5 – нет решений, т.к | sin![]() |
| ![]() 1
1
x = ![]() +
+ ![]() к; к
к; к ![]() Z.
Z.
Ответ: x = ![]() +
+ ![]() к , к
к , к ![]() Z.
Z.
2 ученик. 2 способ. Решение уравнений преобразованием суммы или разности тригонометрических функций в произведение
cos 3x + sin 2x – sin 4x = 0.
Для решения уравнения воспользуемся формулой sin![]() – sin
– sin![]() = 2 sin
= 2 sin![]() сos
сos![]()
cos 3x + 2 sin![]() сos
сos![]() = 0,
= 0,
сos 3x – 2 sin x cos 3x = 0,
cos 3x (1 – 2 sinx) = 0. Полученное уравнение равносильно совокупности двух уравнений:
![]()
![]()
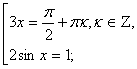
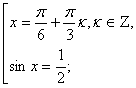


Множество решений второго уравнения полностью входит во множество решений первого уравнения. Значит ![]()
Ответ: ![]()
3 ученик. 3 способ. Решение уравнений преобразованием произведения тригонометрических функций в сумму
sin 5x cos 3x = sin 6x cos2x.
Для решения уравнения воспользуемся формулой ![]()

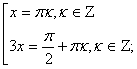
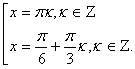
![]()
Ответ: ![]()
4 ученик. 4 способ. Решение уравнений, сводящихся к квадратным уравнениям
3 sin x – 2 cos2x = 0,
3 sin x – 2 (1 – sin2x ) = 0,
2 sin2x + 3 sin x – 2 = 0,
Пусть sin x = t, где | t |![]() . Получим квадратное уравнение 2t2 + 3t – 2 = 0,
. Получим квадратное уравнение 2t2 + 3t – 2 = 0,
D = 9 + 16 = 25.
![]() . Таким образом
. Таким образом 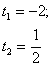 .
. ![]() не удовлетворяет условию | t |
не удовлетворяет условию | t |![]() .
.
Значит sin x = ![]() . Поэтому
. Поэтому ![]() .
.
Ответ: ![]()
III. Закрепление изученного по учебнику А. Н. Колмогорова
1. № 164 (а), 167 (а) (квадратное уравнение)
2. № 168 (а) (разложение на множители)
3. № 174 (а) (преобразование суммы в произведение)
4. ![]() (преобразование произведения в сумму)
(преобразование произведения в сумму)
(В конце урока показать решение этих уравнений на экране для проверки)
№ 164 (а)
2 sin2 x + sin x – 1 = 0.
Пусть sin x = t, | t | ![]() 1. Тогда
1. Тогда
2 t2 + t – 1 = 0, t![]() = – 1, t
= – 1, t![]() =
= ![]() . Откуда
. Откуда 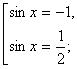

Ответ: –![]() .
.
№ 167 (а)
3 tg2 x + 2 tg x – 1 = 0.
Пусть tg x = 1, тогда получим уравнение 3 t2 + 2 t – 1 = 0.
![]()
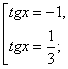

Ответ: ![]()
№ 168 (а )

Ответ: ![]()
№ 174 (а )
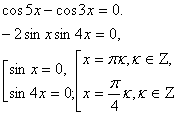
Ответ: ![]()
Решить уравнение: ![]()

Ответ: ![]()
2 урок (урок-лекция)
IV. Изучение нового материала (продолжение)
– Итак, продолжим изучение способов решения тригонометрических уравнений.
5 способ. Решение однородных тригонометрических уравнений
Уравнения вида a sin x + b cos x = 0, где a и b – некоторые числа, называются однородными уравнениями первой степени относительно sin x или cos x.
Рассмотрим уравнение
sin x – cos x = 0. Разделим обе части уравнения на cos x. Так можно сделать, потери корня не произойдёт, т.к. , если cos x = 0, то sin x = 0. Но это противоречит основному тригонометрическому тождеству sin2 x + cos2 x = 1.
Получим tg x – 1 = 0.
tg x = 1,
![]()
Ответ: ![]()
![]()
Уравнения вида a sin2 x + bcos2x + c sin x cos x = 0 , где a, b, c –некоторые числа, называются однородными уравнениями второй степени относительно sin x или cos x.
Рассмотрим уравнение
sin2x – 3 sin x cos x + 2 cos2 = 0. Разделим обе части уравнения на cos x, при этом потери корня не произойдёт, т.к. cos x = 0 не является корнем данного уравнения.
tg2 x – 3tg x + 2 = 0.
Пусть tg x = t. D = 9 – 8 = 1.
![]() тогда
тогда ![]() Отсюда tg x = 2 или tg x = 1.
Отсюда tg x = 2 или tg x = 1.
В итоге x = arctg 2 + ![]()
![]() , x =
, x = ![]()
Ответ: arctg 2 + ![]()
![]() ,
,![]()
Рассмотрим ещё одно уравнение: 3 sin2x – 3 sin x cos x + 4 cos2 x = 2.
Преобразуем правую часть уравнения в виде 2 = 2 · 1 = 2 · (sin2x + cos2x). Тогда получим:
3sin2x – 3sin x cos x + 4cos2 x = 2 · (sin2x + cos2 x),
3sin2x – 3sin x cos x + 4cos2x – 2sin2x – 2 cos2x = 0,
sin2x – 3sin x cos x + 2cos2x = 0. (Получили 2 уравнение, которое уже разобрали).
Ответ: arctg 2 + ![]() k,
k,![]()
6 способ. Решение линейных тригонометрических уравнений
Линейным тригонометрическим уравнением называется уравнение вида a sin x + b cos x = с, где a, b, c – некоторые числа.
Рассмотрим уравнение sin x + cos x = – 1.
Перепишем уравнение в виде: ![]()
Учитывая, что ![]() и
и![]() , получим:
, получим:
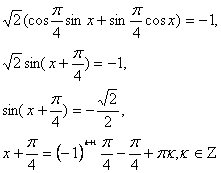
![]()
![]()
Ответ: ![]()
7 способ. Введение дополнительного аргумента
Выражение a cos x + b sin x можно преобразовать:
![]() .
.
(это преобразование мы уже ранее использовали при упрощении тригонометрических выражений)
Введём дополнительный аргумент – угол ![]() такой, что
такой, что 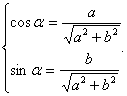
Тогда ![]()
![]()
Рассмотрим уравнение: 3 sinx + 4 cosx = 1.
Учтём, что ![]() . Тогда получим
. Тогда получим ![]()
0,6 sin x + 0,8 cosx = 1. Введём дополнительный аргумент – угол ![]() такой, что
такой, что ![]() , т.е.
, т.е. ![]() = arcsin 0,6. Далее получим
= arcsin 0,6. Далее получим 
Ответ: – arcsin 0,8 + ![]() +
+ ![]()
8 способ. Уравнения вида Р![]()
Такого рода уравнения удобно решать при помощи введения вспомогательной переменной t = sin x ± cosx. Тогда 1 ± 2 sinx cosx = t2.
Решить уравнение: sinx + cosx + 4 sinx cosx – 1 = 0.
Введём новую переменную t = sinx + cosx, тогда t2 = sin2x + 2sin x cos x + cos2 = 1 + 2 sin x cos x Откуда sin x cos x = ![]() . Следовательно получим:
. Следовательно получим:
t + 2 (t2 – 1) – 1 = 0.
2 t2 + t – 2 – 1 = 0,
2 t2 + t – 3 = 0..Решив уравнение, получим ![]() = 1,
= 1, ![]() =
=![]() .
.
sinx + cosx = 1 или sinx + cosx = ![]()
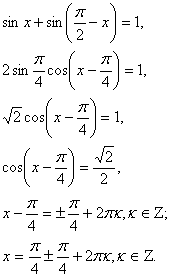
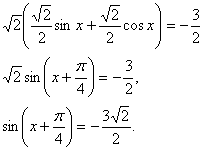
Корней нет.
Ответ: ![]()
9 способ. Решение уравнений, содержащих тригонометрические функции под знаком радикала.
Решить уравнение: ![]()
В соответствии с общим правилом решения иррациональных уравнений вида![]() , запишем систему, равносильную исходному уравнению:
, запишем систему, равносильную исходному уравнению: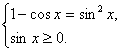
Решим уравнение 1 – cos x = 1 – cos2x.
1 – cos x = 1 – cos2x,
1 – cos x – (1 – cos x) (1 + cos x) = 0,
(1 – cos x) (1 – 1 – cos x) = 0,
– (1 – cos x) cos x = 0.
![]()
![]()
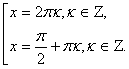
Условию ![]() удовлетворяют только решения
удовлетворяют только решения![]()
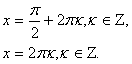
Ответ: ![]()
10 способ. Решение уравнений с использованием ограниченности тригонометрических функций y = sin x и y = cos x.
Решить уравнение: sin x + sin 9x = 2.
Так как при любых значениях х sin x ![]() 1, то данное уравнение равносильно системе:
1, то данное уравнение равносильно системе:![]()
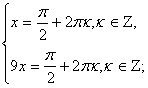
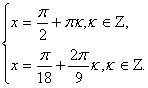
Решение системы ![]()
Ответ: ![]()
V. Итог урока
Таким образом мы сегодня рассмотрели 10 различных способов решения тригонометрических уравнений. Безусловно, многие из приведённых задач могут быть решены несколькими способами.
(Пятерым наиболее подготовленным учащимся , а также всем желающим дать индивидуальное творческое задание: найти различные способы решения тригонометрического уравнения sinx + cosx = 1 )
Домашнее задание: № 164 -170 (в, г).
х решения"
Комментариев нет:
Отправить комментарий