Группа 108

         Показательные уравнения приемы их решения

Методы решения показательных уравнений

• Удовицкая Марина Викторовна, учитель математики

Разделы: Математика

---

Методы решения показательных уравнений

1. Простейшие показательные уравнения

Тип уравнения	Вид уравнения	Метод решения
1		(x)
2		b = a	b b>0	b b
		=  f(x) = 1	f(x) =	Решений нет

Примеры.

Пример 1. Решите уравнение: 34x-5 = 3x+4 .

Решение.

34x-5 = 3x+4 <=> 4x 5 = x+4 <=> 3x=9<=> x = 3 .

Ответ:3

Пример 2. Решите уравнение: 2x-4 = 3 .

Решение.

2x-4 = 3 <=> x- 4 =   x =  + 4 <=> x =  +  <=> x =  .

Ответ:.

Пример 3. Решите уравнение:-3x = -7 .

Решение.

-3x = -7 , решений нет, так как -3x > 0 для  x  R .

Ответ: .

2. Методы преобразования показательных уравнений к простейшим.

A. Метод уравнивания оснований.

Примеры.

Пример 1. Решите уравнение: 27- = 0 .

Решение.

27- = 0 <=> 3334x-9- (32)x+1 = 0 <=> 33+ (4x-9)- 32(x+1) = 0<=> 34x-6-32x+2 = 0 <=> 34x-6 = 32x+2<=> 4x-6=2x+2 <=> 2x = 8 <=> x=4.

Ответ: 4.

Пример 2. Решите уравнение:  .

Решение.

 0 <=> (22)x3x5x = 604x-15 <=> 4x3x5x = 604x-15 <=> (4x = 604x-15 <=> 60x=604x-15 <=> <=>x=4x-15 <=> 3x=15 <=> x=5.

Ответ: 5.

В. Уравнения, решаемые разложением на множители.

Примеры.

Пример 1. Решите уравнение: x2x = 22x + 8x-16.

Решение.

x2x = 22x + 8x-16 <=> x2x - 22x = 8x-2) <=> 2x(x-2) - 8 <=> (x-2) x - 8) = 0 <=>  <=>  <=>  <=>  .

Ответ: 

Пример 2 . Решите уравнение: 

Решение.

52x - 7x - 52x35 +7x = 0 <=> (52x - 7x)((

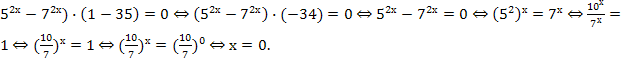
Ответ: 0.

С. Уравнения, которые с помощью подстановки f(x) = t, t>0 преобразуются к квадратным уравнениям (или к уравнениям более высоких степеней).

Пусть  , где А, В, С - некоторые числа. Сделаем замену:  >0, тогда A2 + B + C = 0

Решаем полученное уравнение, находим значения t, учитываем условие t >0 , возвращаемся к простейшему показательному уравнению f(x) = t, решаем его и записываем ответ.

Примеры.

Пример 1 . Решите уравнение: 22+x - 22-x = 5.

Решение.

22+x - 22-x = 5 <=> 222x -  = 15 <=> 4(2x)2 - 4 = 15x

Делаем замену t = 2x, t > 0. Получаем уравнение 42 - 4 = 15t <=> 4t2 - 15t - 4=0

<=>  , t =  не удовлетворяет условию t > 0.

Вернемся к переменной х:

2х = 4<=> 2x = 22 <=> x=2.

Ответ: 2

Пример 2. Решите уравнение: 

Решение.

5

Делаем замену:  , тогда Получаем уравнение:

5 , t = не удовлетворяет условию t 

Вернемся к переменной Х:

Ответ: 2.

D. Уравнения, левая часть которых имеет вид A  nx + B  kx  bmx + С  bnx, где k, m  N, k + m = n

Для решения уравнения такого типа необходимо обе части уравнения разделить либо на nx, либо на nx и получится уравнение типа С).

Примеры.

Пример 1. Решите уравнение: 222x - 5x + 332x = 0.

Решение.

222x - 5x + 332x = 0 <=> 22x - 5x3x + 332x = 0 <=> 2 -  + 3 = 0 <=>

<=> 22x - 5x + 3 = 0

Пусть t = x, t>0 , тогда 2t- 5t + 3 = 0 <=>  , оба значения t удовлетворяют условию t Вернемся к переменной х:

 <=>  <=>  .

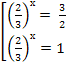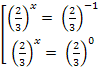Ответ: 

Пример 2. Решите уравнение: 8x + 18x - 227x = 0 .

Решение.

8x + 18x - 227x = 0 <=>  +  - 2 = 0 <=> 23x + 2x 32x - 233x = 0<=>

<=>  +  - 2 = 0 <=>  +  - 2 = 0.

Пусть  = t, t>0 , тогда t3 + t - 2 = 0<=> (t3 - 1) + (t -1 )= 0 <=> (t-1) (t2 +t +1) + (t - 1) <=> (t - 1) (t2 + t +2) = 0 <=> 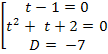 <=> t - 1= 0 <=> t=1. (t>0)

Вернемся к переменной х:  = 1 <=> =  x = 0 .

Ответ: 0.

К данному типу уравнений относятся уравнения , левая часть которых имеет вид , где А, В, С -некоторые числа, причем .

Уравнения такого типа решаются с помощью подстановки :

= t , тогда =  .

Пример 3. Решите уравнение: 

Решение.

Заметим, что произведение оснований степени равно единице:

(. Поэтому можно ввести новую переменную: , причем . Получим уравнение:

t ,оба корня удовлетворяют условию :.

Вернемся к переменной х:

 .

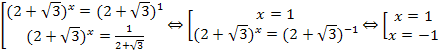Ответ: .

Е. Уравнения, имеющие вид Aam = Bbm.

Для решения необходимо обе части уравнения разделить либо на am, либо на bm. В результате получается простейшее уравнение.

Примеры.

Пример 1. Решите уравнение: 7х = 5х.

Решение.

7х = 5х <=>  = 1 <=>  =  <=> x = 0.

Ответ: 0.

Пример 2. Решите уравнение: .

Решение.

.

Ответ: 2.

F. Метод, основанный на использовании свойства монотонности показательной функции .

Примеры.

Пример 1. Решите уравнение:  .

Решение.

Заметим, что при х=1 уравнение обращается в тождество. Следовательно, х=1 - корень уравнения. Перепишем уравнение в виде

 (*)

Так как при основании, меньшем единицы, показательная функция убывает на R, то при х левая часть уравнения (*) больше единицы, то есть

Если то левая часть уравнения меньше единицы, то есть

Поэтому, других корней, кроме х=1, уравнение  не имеет.

Ответ: 1.

Пример 2. Решите уравнение:  .

Решение.

Это уравнение также обращается в тождество при х=1.

Перепишем уравнение в виде:

 .

При основании, меньшем единицы, показательная функция убывает на R.

Поэтому при х а при х: . Таким образом, других корней, кроме х=1 , уравнение  не имеет.

Ответ: 1.

G. Графический способ решения уравнений вида f(x).

Чтобы графически решить уравнение такого вида, необходимо построить графики функций y=f(x) в одной системе координат и найти (точно или приближенно) абсциссы точек (если они есть) пересечения этих графиков. Абсциссы этих точек - корни данного уравнения (точность результатов определяем только после подстановки в уравнение ).

Примеры.

Пример 1. Решите уравнение: .

Решение.

1.Рассмотрим две функции: f(x) =  и g(x) = x+1.

2.Графиком функции f(x) =  является кривая, расположенная в верхней полуплоскости, графиком функции g(x) = x+1 является прямая.

3. Зададим таблицы значений этих функций:

х		-1		0	1	2	3
f(x) =					1	2	4
х	0		3
g(x)= x+1	1		4

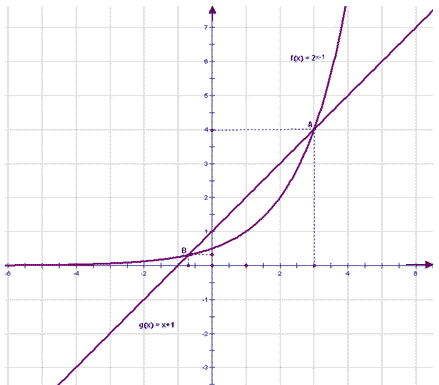
4. Из рисунка видно, что прямая и кривая пересекаются в двух точках- в точке А и в точке В. По графику определяем абсциссы этих точек:  . Значит, уравнение имеет два корня: х=3 и х= . Число х=3 - точный корень заданного уравнения, так как при подстановке в это уравнение получается верное числовое равенство:

Ответ: 3;  .

Пример 2. Решите уравнение:  .

Решение.

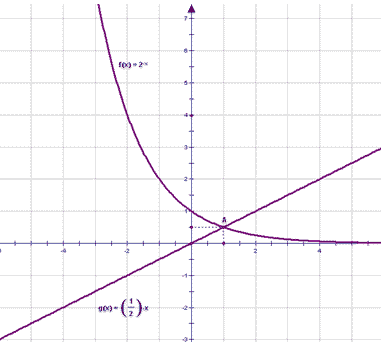
1. Рассмотрим две функции f(x) =  и g(x) = .Используем свойства степени и преобразуем выражение :

 = , тогда вторую формулу можно переписать в виде: f(x) = .

2. Функция f(x) = - показательная по основанию  и ее графиком является кривая, расположенная в верхней полуплоскости.

Функция g(x) =- прямая пропорциональность и ее график - прямая, проходящая через точку .

3. Зададим таблицы значений этих функций и затем построим их графики в одной системе координат.

х	-3			-2	-1	0	1	2
f(x) =	8			4	2	1
х		1	4
g(x) =			2

4. Графики пересекаются в одной точке - в точке А, ее абсцисса равна единице.Значит, х=1 - корень заданного уравнения.

Примечание:

Если одна часть уравнения содержит убывающую функцию f(x) , а другая часть -возрастающую функцию g(x), и уравнение имеет корень х=, то он -единственный.

В примере 2. : f(x) = убывающая на R функция, а g(x = - возрастающая на R функция, х=1- корень уравнения и он